台形面積 208334-台形面積 公式

台形の面積計算 ゆるゆるプログラミング

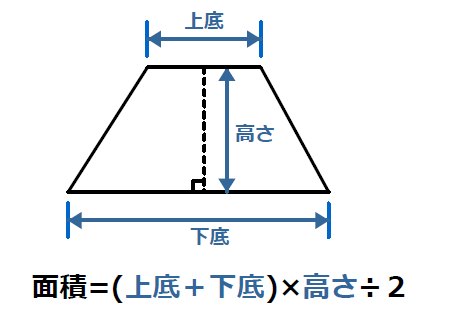
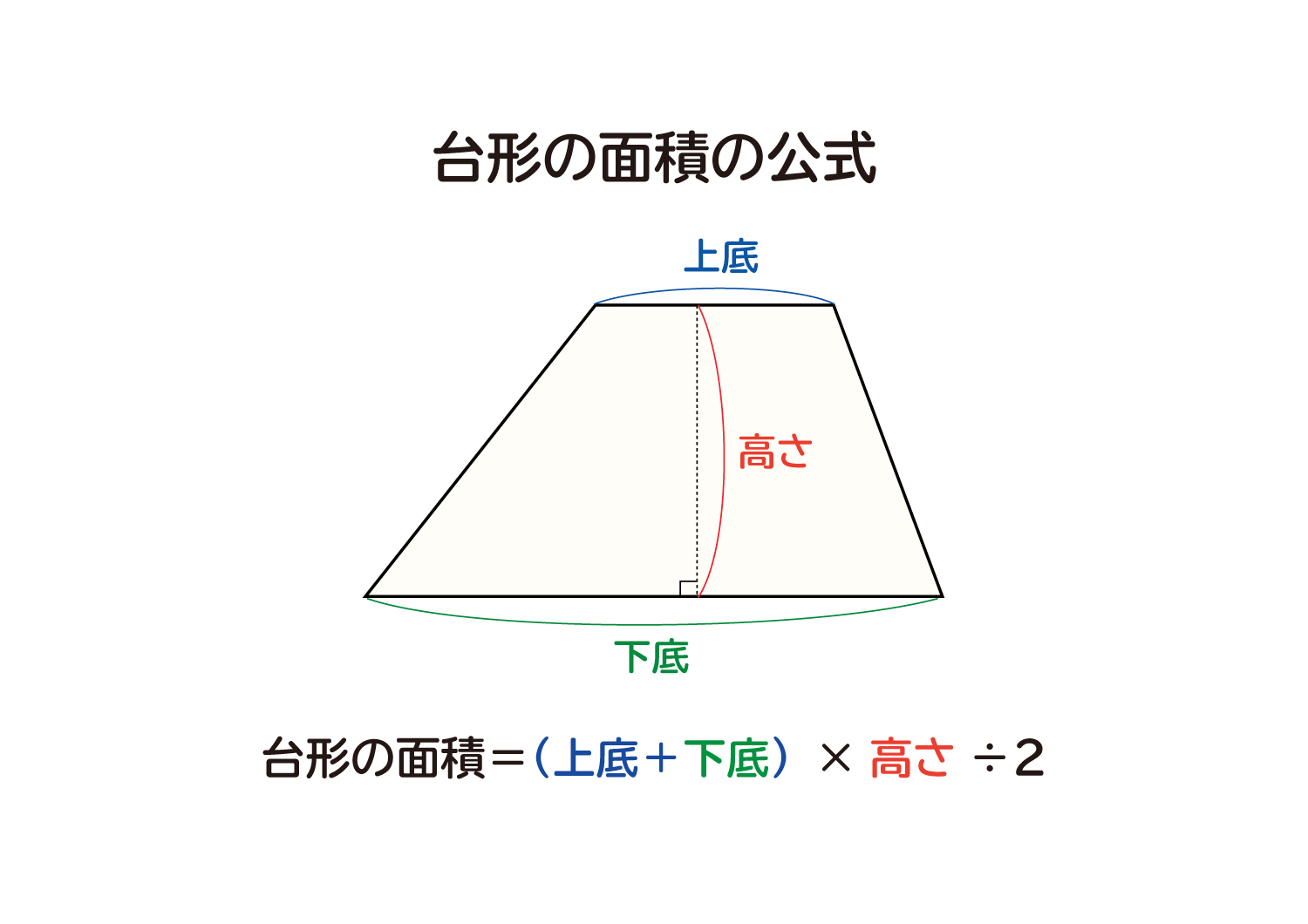
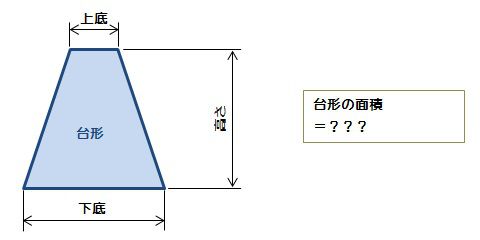
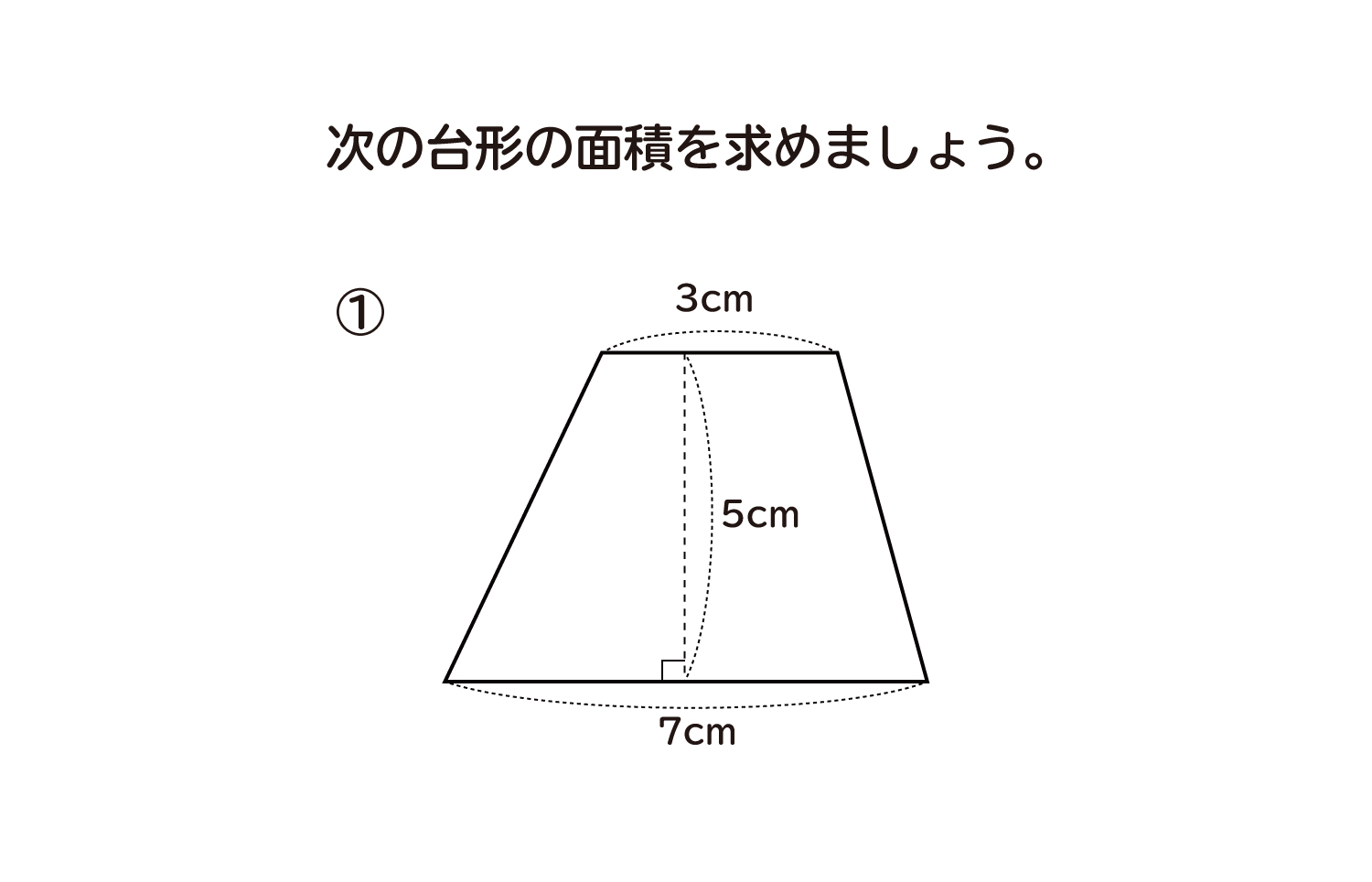
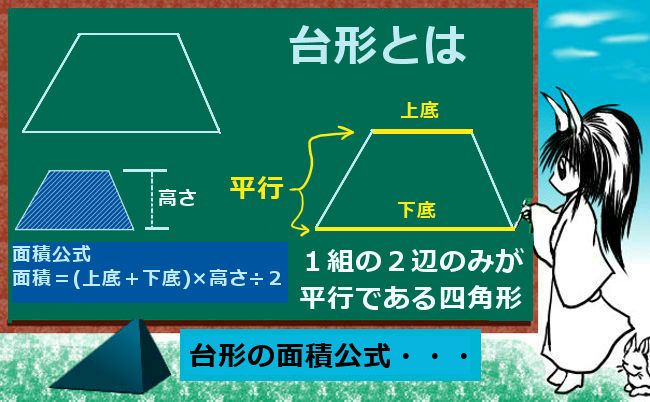
台形の面積の公式 台形の面積は 『（上底下底）×高さ÷2 ÷ひし形の面積は、この直角三角形の面積の4倍なので \(ひし形=直角三角形×4=(たて×横÷8)×4\) \(=たて×横÷2\) となり、ひし形の面積の公式が求まります。 ④ 台形の面積 台形の面積は、\(「面積=(上底下底)×高さ÷2」\) で求められます。

台形面積 公式

台形面積 公式-台形の面積の求め方を教えて下さい 上底の長さが2cm 高さが25cm 台形左の斜線が3cmです 下底はわからない状態です。 数学 台形の体積の求め方を教えてください 上底 3 下底 7 高さ10 斜面 1：05 です 面積はわかるのですが体積の計算式がまったくわかりません台形の面積を求める公式は、s = {(上底)(下底)}×(高さ)÷2 で表されます。このページでは、台形の面積の求め方を、計算問題と共に説明しています。また、公式の導き方も説明しています。

高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

ひし形の面積を求める公式は ひし形の面積 対角線 対角線 ひ し 形 の 面 積 = 対 角 線 ×面積の計算 ・ 正三角形の面積 ・ 三角形の面積 (底辺と高さ) ・ 三角形の面積 (2辺と間の角度) ・ 三角形の面積 (1辺と両端の角度) ・ 三角形の面積 (3辺の長さ) ・ 正方形の面積 ・ 長方形の面積 ・ 台形2 なので、 ひし形の面積 ひ し 形 の 面 積 = 8 ×

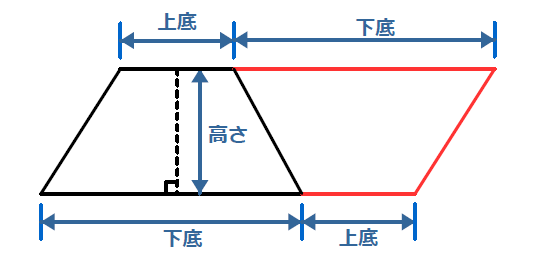
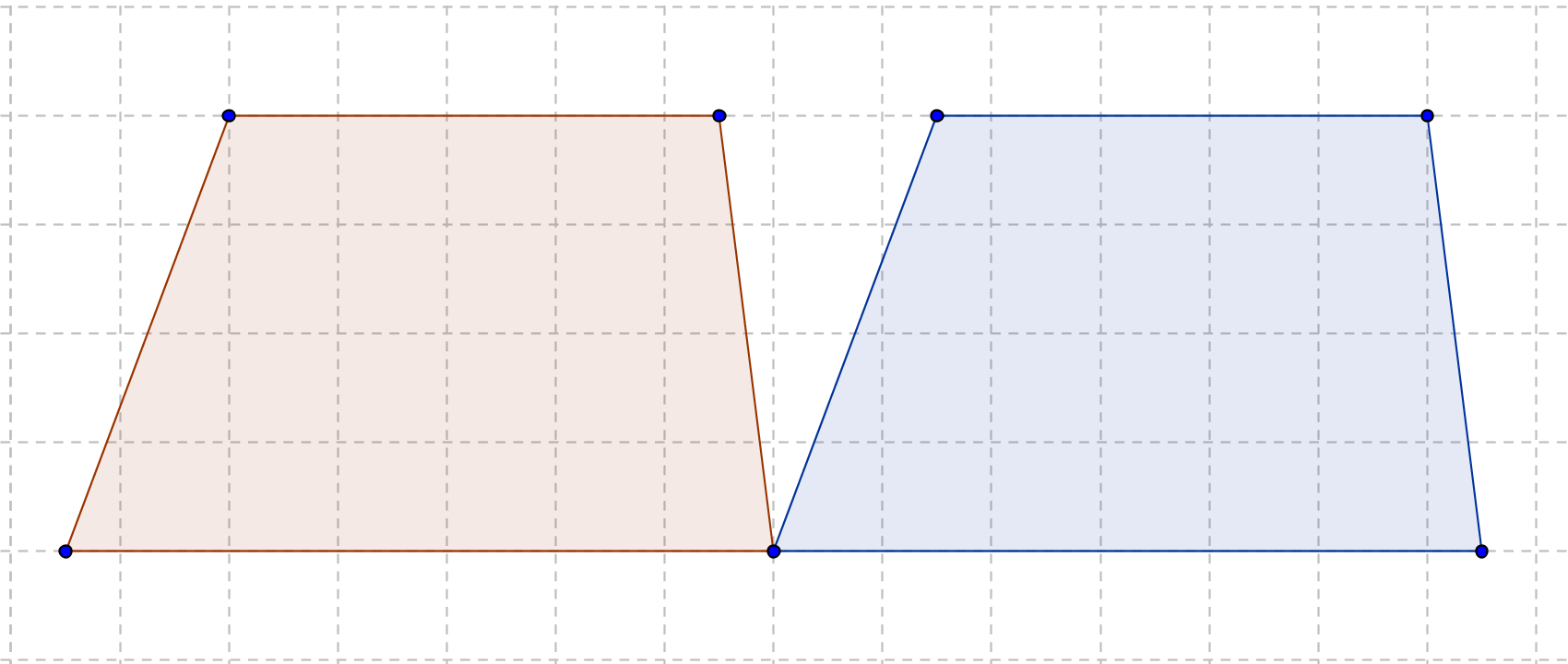
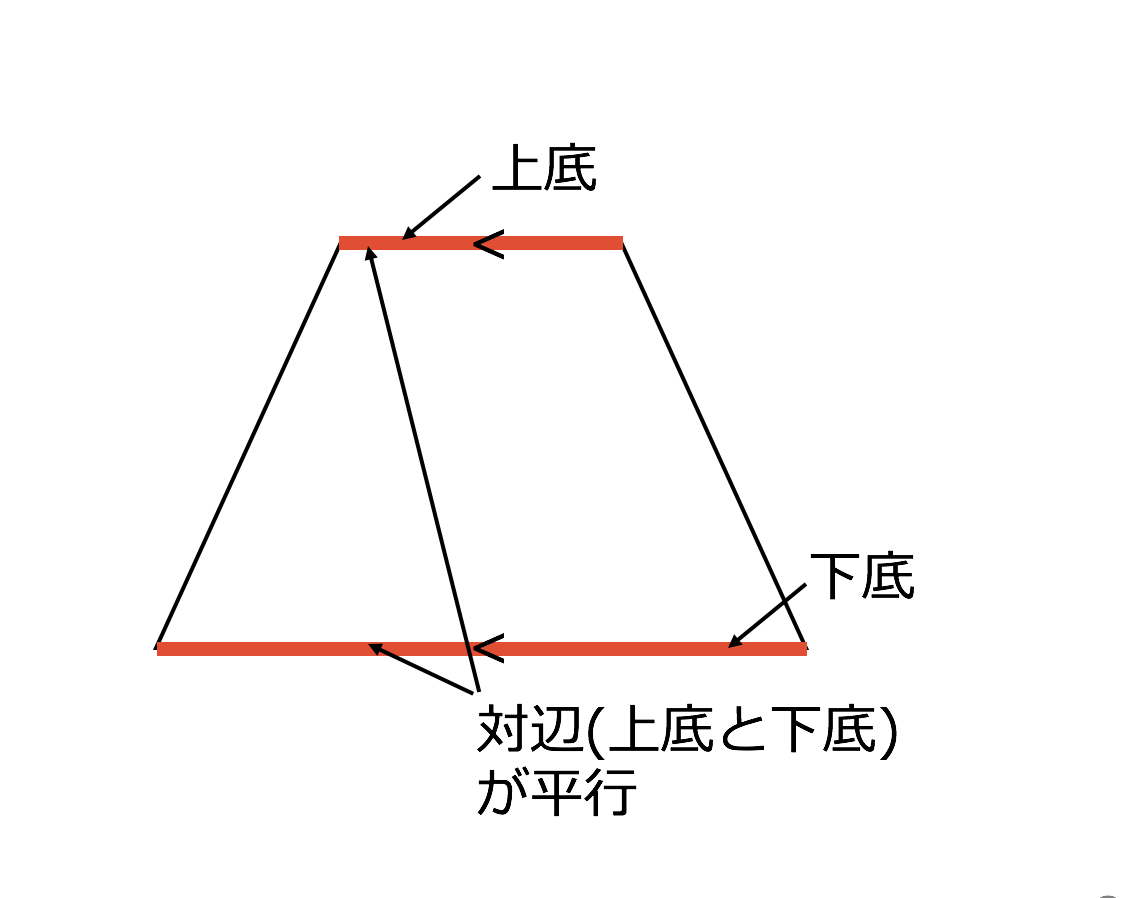
「台形の面積」計算機は、台形の面積をWeb上でカンタンに計算できる電卓です。計算機は2つ用意しました。一つは、基本の公式で求めるパターン。( 上底 下底 ) x 高さ ÷台形の面積の計算方法です。台形は、四角形のうち、一対の辺が平行になっているものです。平行になっている辺を上下に置くと、台のようになりますね。台形は、ラテン語でトラペジウムと呼びます。 面積の計算方法は (上底 下底) x 高さ ÷台形の面積は、平行四辺形の面積の半分なので（上底＋下底）×高さ÷2となります。 ここでは、キーボードから上底と下底と高さを入力して、台形の面積を表示するプログラムを紹介します。 AreaofTrapezoid1java ← クリックしてダウンロードページに移動

台形面積 公式のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	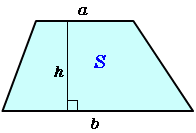Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	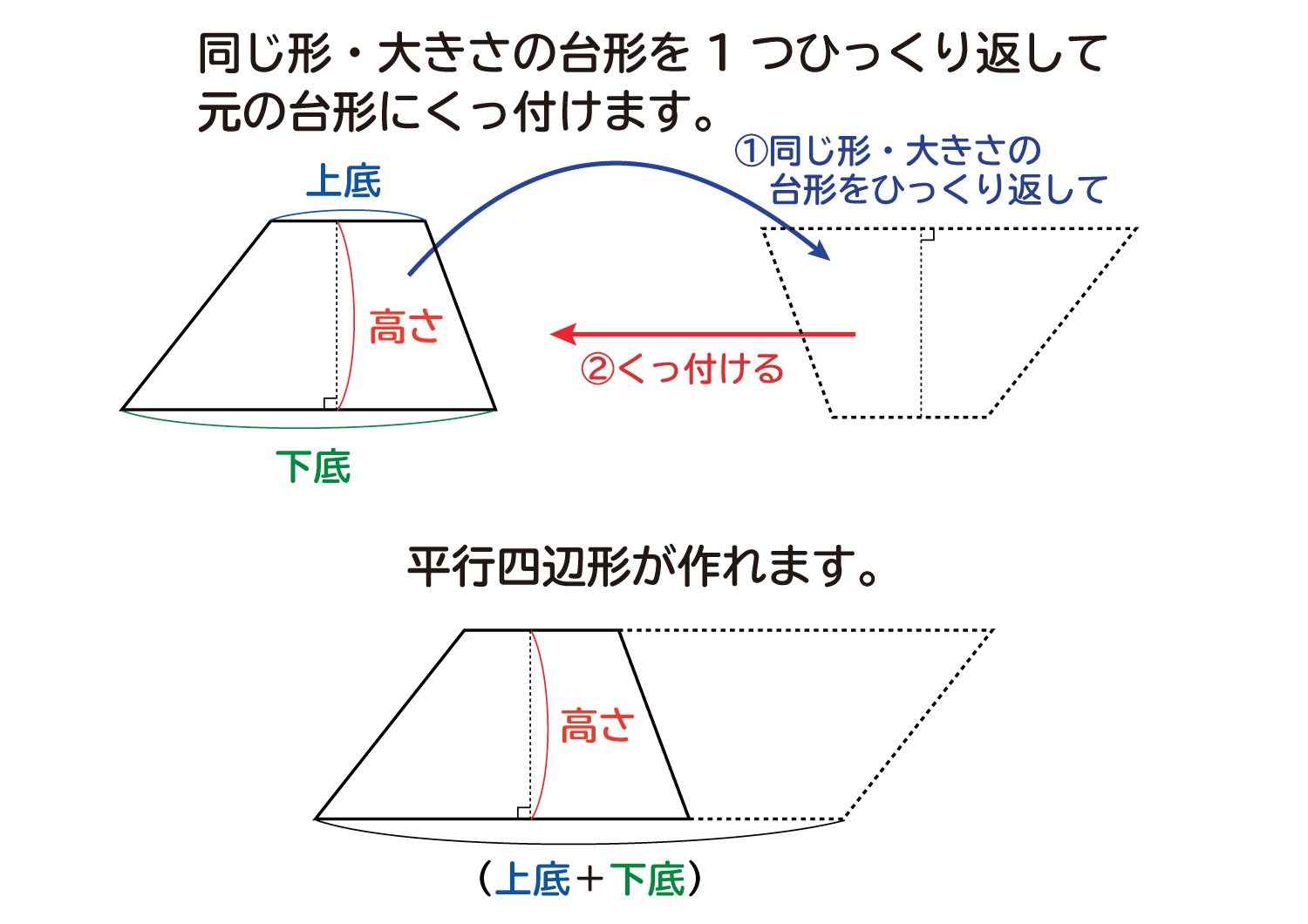Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	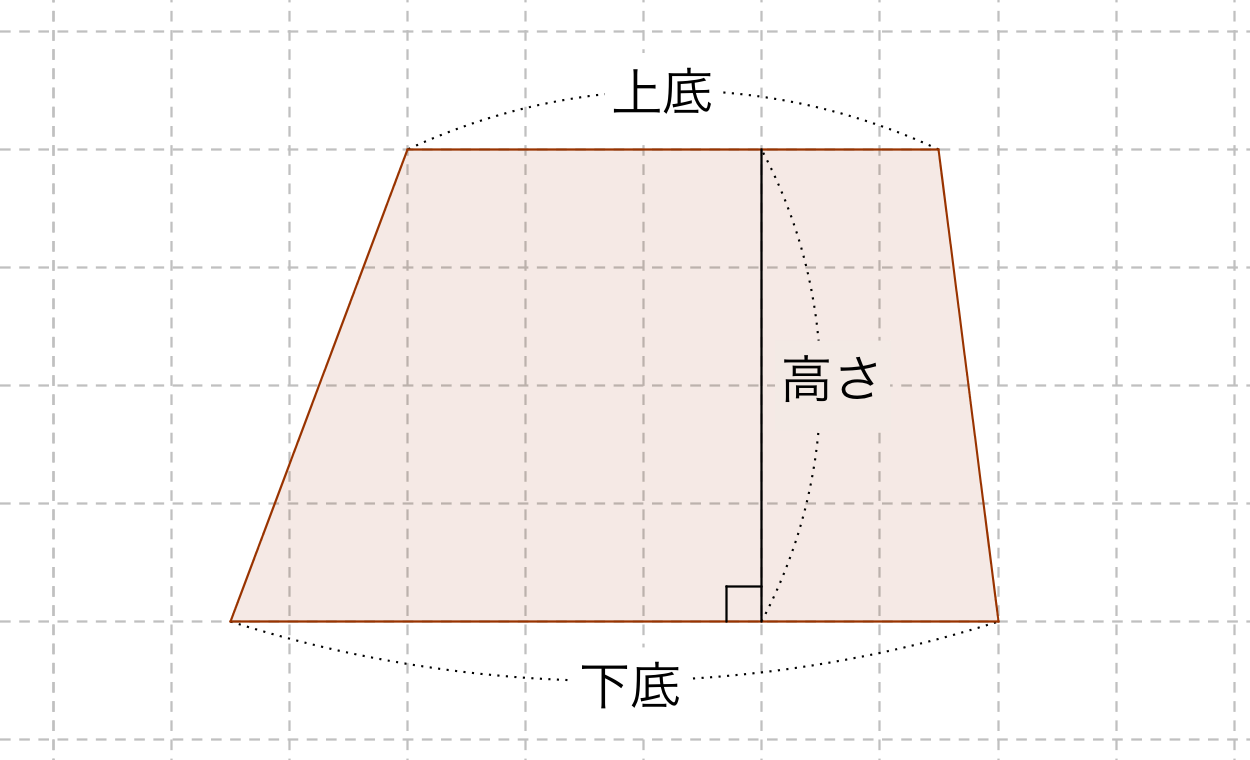Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	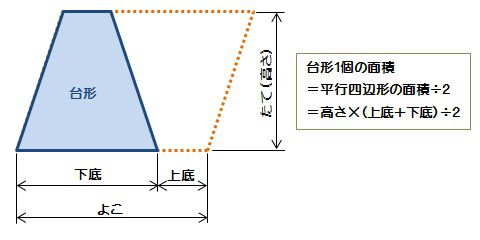Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	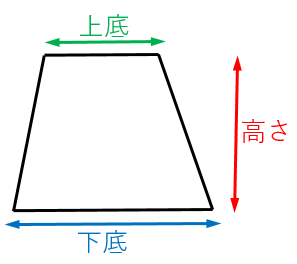Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	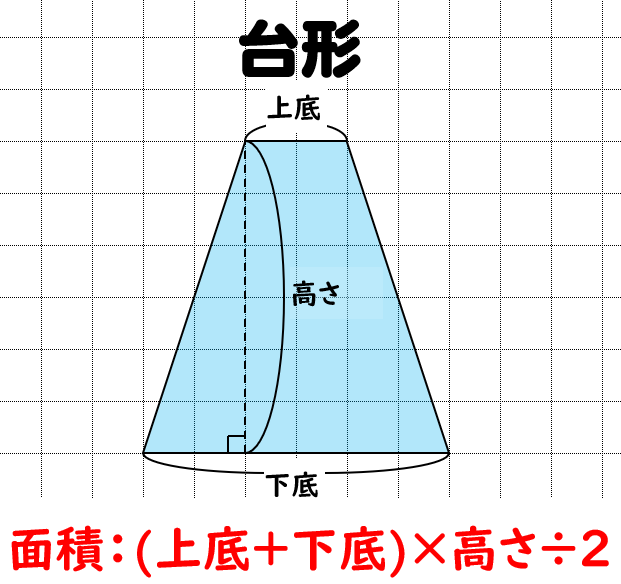Trapezoidal Area Stock Illustration	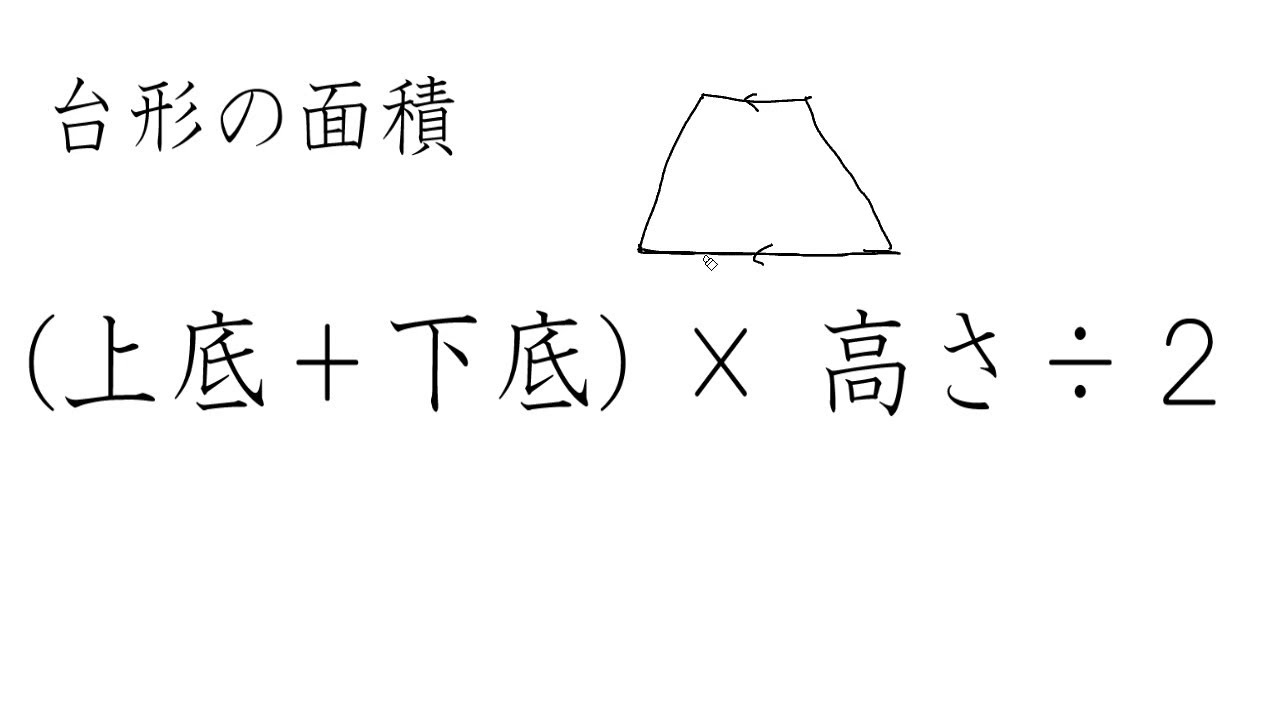Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	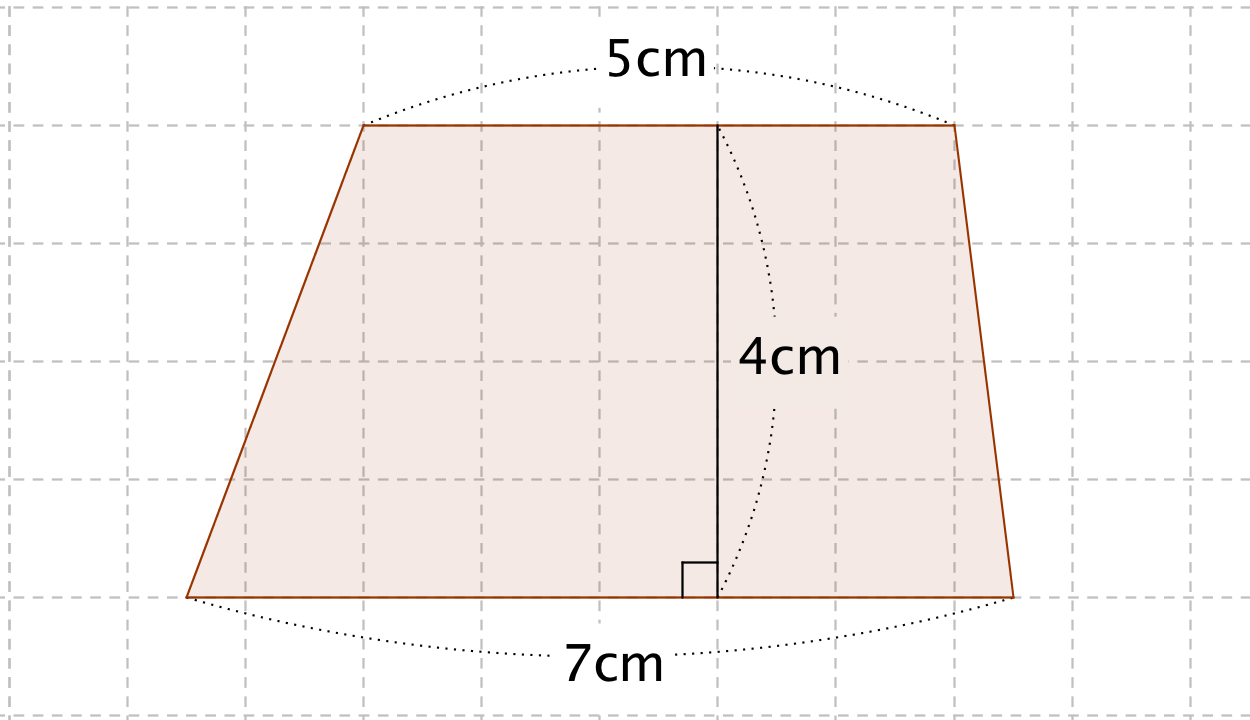Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	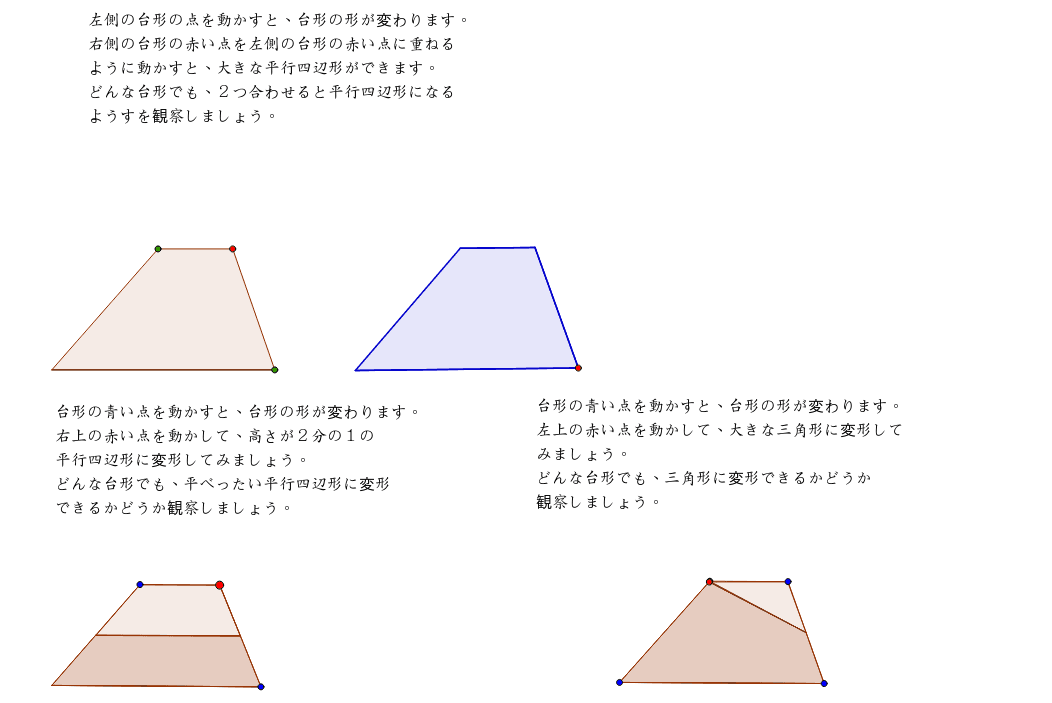Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	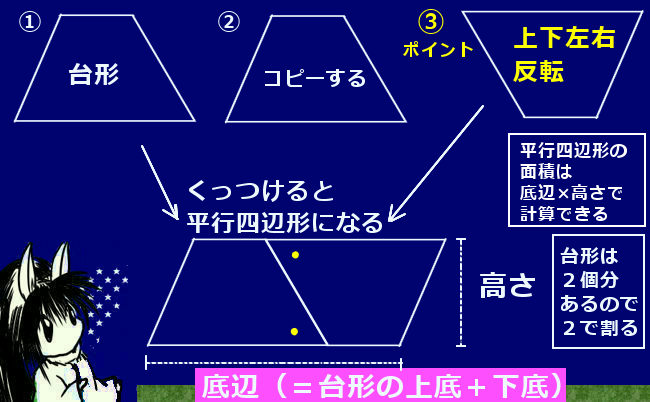Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	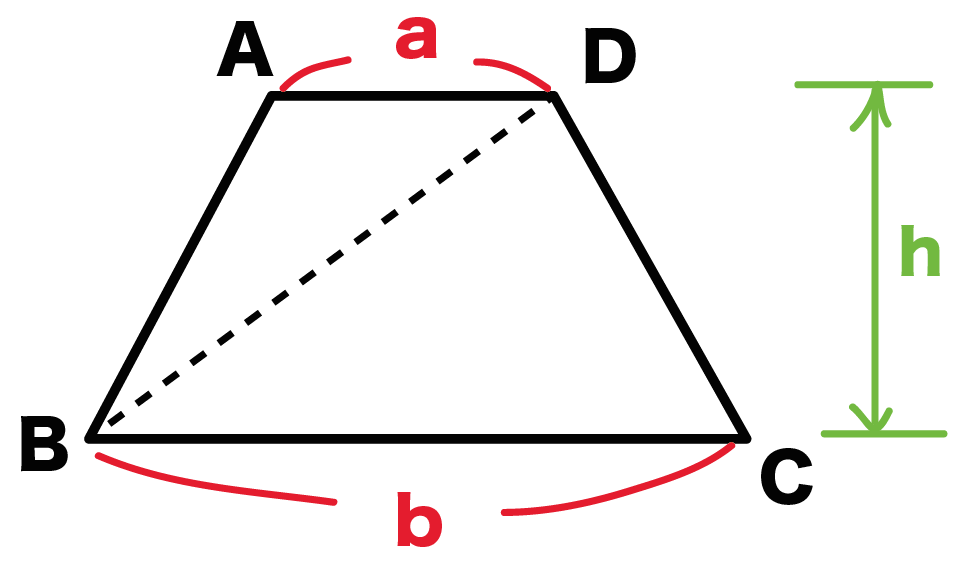Trapezoidal Area Stock Illustration	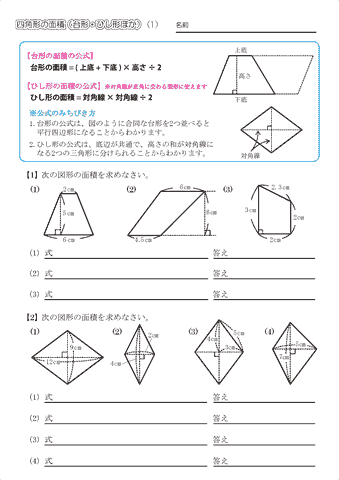Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	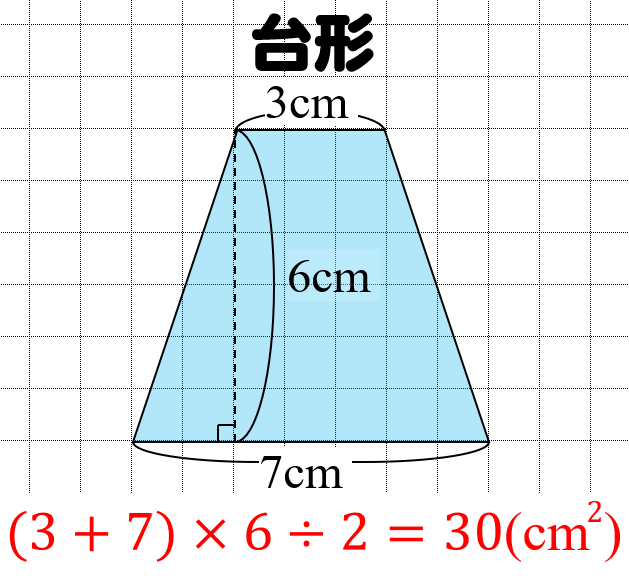Trapezoidal Area Stock Illustration	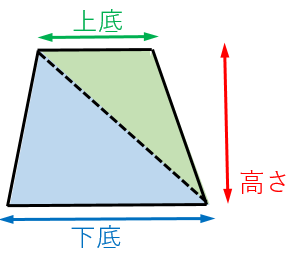Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	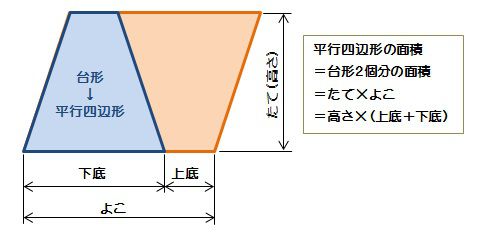Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration
Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration	Trapezoidal Area Stock Illustration

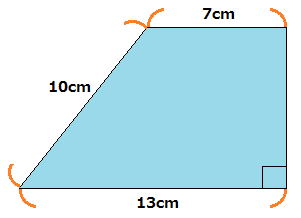
6÷2＝30(cm2) ( 3 7) ×台形の体積の求め方 を教えてほしい。 そう、きかれることが結構ある。 正直ドヤ顔で、 台形の体積はね・・・ って答えそうになる。 だけれども、 そもそも台形に体積はないんだ！ 台形は平面図形だからね。 台形の面積なら求められるけど、体積は無理

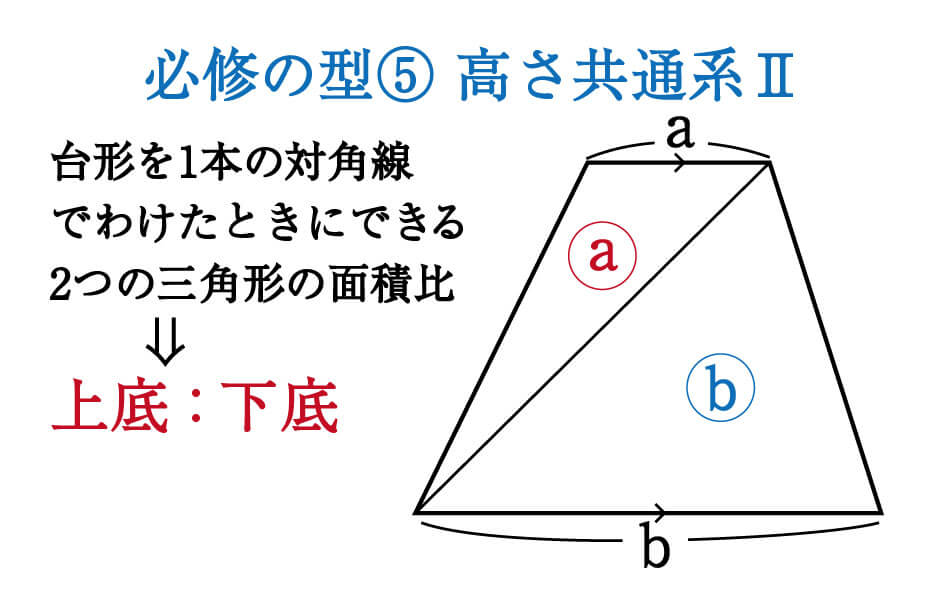
Incoming Term: 台形面積, 台形 面積 公式 小学生, 台形面積 公式, 台形面積 求め方, 台形面積 計算, 台形面積 エクセル, 台形面積 高さがわからない, 台形面積 問題, 台形面積 なぜ, 台形面積 対角線,